خواص الدائرة وحساب الزوايا المختلفة بأفضل طريقة
سنتعرف في هذا المقال إن شآءالله عن:
- بعض خواص الدائرة
- أمثلة على خواص الدائرة المتنوعة
- الخواص المتعلقة في الدائرة ومحيطها.
- مفهوم مماسات الدائرة.
- التعرف على أهمية خواص الدائرة وفوائدها.
يُمكن تعريف خواص الدائرة Sphere
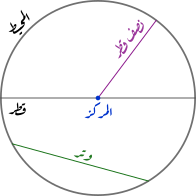
الدائرة هي الشكل الهندسي المكون من مجموعة من النقاط التي تقع على بُعد ثابت من نقطة محددة و ثابتة والمتصلة فيما بينها لتشكل خط منحني مغلق ، وتُعرف عادة هذه النقطة باسم مركز الدائرة أو مركز ثقل الدائرة ،وللدائرة نصف قطر وهو البُعد أو المسافة من مركز الدائرة إلى أيّة نقطة على محيطها أو هو المسافة بين مركز الدائرة وأي نقطة من محيط هذه الدائرة وهو دائماً ثابت في الطول في الدائرة الواحدة ويُرمز له بالرمز R
بينما يعرف قطر الدائرة على أنه الخط الواصل بين أي نقطتين من محيط الدائرة بشرط مرور هذا الخط من مركز هذه الدائرة ، ويعدها الخط أطول وتر في الدائرة ويُرمز به بالرمز D ، والقطر ونصف القطر مترابطان حيث إنّ القطر يعادل ضعف نصف القطر تماماً لأن أقطار الدائرة متجانسة ومتطابقة ، D=2 R
خصائص القطع المستقيمة المتعلقة بالدائرة
من أشهر القطع المستقيمة المتعلقة بالدائرة وخصائصها ما يأتي:
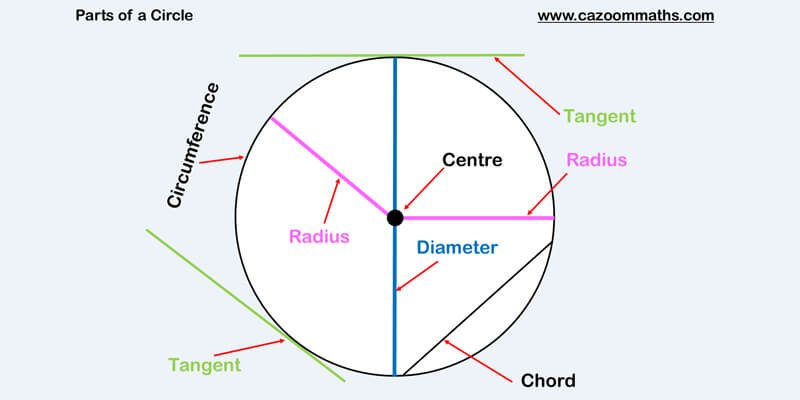
الوتر: Chord هو القطعة المستقيمة الواصلة بين نقطتين على حدود الدائرة، ويقسم الخط العمودي الساقط من مركز الدائرة الوتر إلى قسمين متساويين، ومن أهمّ خواص الوتر في الدائرة :
المماس: Tangent وهو القطعة المستقيمة التي تمس محيط الدائرة بنقطة واحدة فقط ومن خواص مماس الدائرة :
خواص الدائرة الزوايا التي تتعلق في الدائرة سنتعرف عن أهم الخواص المتعلقة بالدائرة :
الزاوية المحيطيّة Inscribed Angle
هي الزاوية التي تتكون من تلاقي قطعتين مستقيمتين أو وترين على محيط الدائرة ، ومن الخواص :
تتساوى الزوايا المتشكلة على ذات القوس في قياسها.
الزاوية المركزية Central Angle
هي الزاوية التي يكون رأسها على مركز الدائرة أو هي الزاوية المتشكلة من نصفي قطر في هذه الدائرة ويقابها قوس أو جزء من محيط الدائرة لذلك سميت بالمركزية وأيضاً الزاوية المحيطية سميت بهذا الاسم لأنها تقع على محيط الدائرة ، أي نهاية كلّ من أضلاعها أو نصفي القطر يقطعان محيط الدائرة، ومن خواصها :
قياس الزاوية المركزيّة يساوي ضعف قياس الزاوية المُحيطيّة المتشكلة والتي تحصر نفس القوس.
تتساوى الأقواس عندما تشكل زوايا مركزية مُتساوية والعكس صحيح أي الزوايا المركزية اللواتي يحصران نفس طول القوس أو نفس طول الجزء من محيط هذه الدائرة متساويات أيضاً أي كلما زاد قياس الزاوية المركزيّة كان طول القوس المقابل لها أكبر.
إذا كانت الزاوية المركزية= 180 درجة =π فإن القوس الذي تحصره هذه الزاوية أو تشكلهُ يساوي نصف محيط هذه الدائرة.
إذا كانت الزاوية المركزية= 360°=0=π×2 فإن القوس الذي تحصره هذه الزاوية يساوي إلى محيط هذه الدائرة كاملاً ويكون ضلعي هذه الزاوية منطبقين أي الزاوية معدومة أو 3٦٠ درجة..
تتساوى قياس الزوايا التي تقابل أو تحصر نفس القوس
الخواص العامة للدائرة
من الخصائص العامّة للدائرة :
- تتطابق وتتساوى الدوائر إذا كان نصف قطر هذه الدوائر مُتساوٍ في الطول
قطر الدائرة هو أطول وتر في الدائرة أو طول القطعة المستقيمة الواصلة بين نقطتين من محيط الدائرة والمارة بمركز الدائرة
تقل المسافة العمودية بين مركز الدائرة والوتر كلما زاد طول الوتر ويصبح طوله أعظمياً عندما يمر من مركز الدائرة أو ينطبق على قطر من أقطار الدائرة
عند رسم مماسيّن عند نهايتيّ قطر الدائرة فإنّهما منطبقان أو مُتوازيان.
المُثلث الذي يتكون من نصفيّ قطر الدائرة أو أي مثلث يكون فيه ضلعان يمثلان أنصاف أقطار هذه الدائرة، والوتر أو القطعة المستقيمة الواصلة بين طرفي نصفي القطر يكون مُثلثاً مُتساوي الساقين دوماً لأن أنصاف الأقطار في دائرة واحدة متساوية الطول..
إن حاصل قسمة قيمة المُحيط لأيّ دائرة على طول قطرها فإنّ الناتج يكون دائماً قيمة ثابتة تُدعى بي وتساوي حاصل هذه القسمة تقريباً 3.14١٦ أو ٧/٢٢ .
شاهد ايضاً خواص الدائرة وحساب الزوايا المختلفة بأفضل طريقة.
أمثلة عن خواص الدائرة
أمثلة تطبيقية على خواص الدائرة :
المثال الأول: تقاطع وتران AB، CD عند النقطة (O)، حيثُ يُقسّم كل منهما الآخر إلى قسمين ، وفي الوتر الأول كان طول AO= 4 cm سم وطول OB = 6 cm بينما في الوتر الثاني كان طول CO =3cm، فجد طول OD؟
الحل: من خاصيّة تقاطع الأوتار مع بعضها ينتج أنّ: حاصل ضرب أجزاء أو طول الوتر الأول بالواحدات يساوي حاصل ضرب أجزاء أوطول الوتر الثاني ببعضهما أي OD×3=4×6، وبقسمة الطرفين على 3 ينتج أنّ: OD =8cm أو واحدات
المثال الثاني: دائرة مركزها M فيها المماس D يمُسّ الدائرة في النقطة A ويلتقي مع الوتر AB في النقطة A، فإذا كان قياس الزاوية BAD= 60، فما قياس الزاوية AMB؟
الحل:
وفق الخاصة عند التقاء المماس DA الذي يمُسّ الدائرة في النقطة A مع الوتر AB فإنّ الزاوية المتشكلة بينهما تساوي الزاوية المحيطيّة ACB المقابلة للوتر AB وعليه فإن قياس الزاوية المحيطية المقابلة للوتر AB =٦٠ درجة
المثال الثالث: زاوية محيطيّة وزاوية مركزيّة تقابلان نفس القوس، فإذا كان قياس الزاوية المحيطيّة= ٧٥، فما قياس الزاوية المركزيّة؟
الحل: حسب الخاصة الشهيرة أن قياس الزاوية المركزيّة دوماً = ضعف قياس الزاوية المُحيطيّة المرسومة على نفس القوس فإن :
الزاوية المركزيّة =2×٧٥= ١٥٠ درجة
المثال الرابع: دائرة مركزها النقطة m فيها الوتران ab ، ac وقياس الزاوية amb= 90 درجة ، وقياس الزاوية AMc=120، فما قياس الزاوية BAC ؟
الحل: بما أنّ الزاوية AMB + الزاوية AMC + الزاوية CMB = 360، ينتج أن 90+ 120+الزاوية CMB= 360 ومنه الزاوية CMB = 150
وبما أنّ الزاويةجCMB = 2×الزاوية BAC وفق الخاصة : قيمة الزاوية المركزيّة تساوي ضعف قيمة الزاوية المُحيطيّة المتشكلة على نفس القوس لينتج أن 1٥0°=2× الزاوية BAC وبقسمة الطرفين على 2 ينتج أنّ: الزاوية BAC = ٧٥
المثال الخامس: دائرة مركزها النقطة M فيها الوتران AB ، AC وقياس الزاويةBAC = 60 فكم قياس الزاوية MBC؟
الحل: الزاوية BMC = 2× الزاوية BAC وفق الخاصة قيمة الزاوية المركزيّة تساوي ضعف قيمة الزاوية المُحيطيّة الم على نفس القوس؛ لينتج منه أن الزاوية BMC = 2×٦٠= ١٢٠ درجة .
في المثلث المتساوي الساقين MBC ، MB = MC لأنهما أنصاف أقطار في هذه الدائرة، وعليه فإنّ الزاوية MBC = الزاوية MCB .
وبما أنّ مجموع زوايا المثلث يساوي 180 درجة ، ينتج أنّ: MBC + الزاوية MCB + الزاوية BMC =180 ومنه: MBC + الزاوية MCB + 120= 180، وعليه فإنّ: MBCـ + الزاوية MCB=60، بالتالي: 2× الزاوية MBCـ = 60، ومنه الزاوية MBCـ = 30
المثال السادس :إذا كان هناك دائرة مركزها N لديها مماس Lm بالنقطة m، وأن الزاوية LNC= 100 درجة، حيثc نقطة تقع على امتداد خط التماس LM ، جد قياس الزاوية LMN ؟
الحل: من خواص الدائرة مماس الدائرة، أنه يعامد نصف قطر الدائرة أي يشكل زاوية 90 درجة معه وأيضا تشكل مثلث قائم الزاوية لذا يُمكن استخدام خواص الزوايا في مثلث قائم الزاوية لإيجاد قيمة الزاوية NmL الزاوية NLC زاوية خارجية تقع على خط مستقيم، وتعتبر الزاوية NLM متممة لها أي مجموعهما ١٨٠، أي أنّ: الزاوية NLM + الزاوية NLC 100 + الزاوية NLM = 180 الزاوية NLM أحد زوايا المثلث قائم الزاوية = 80 مجموع زوايا المثلث NML القائم في M يساوي 180، أي: الزاوية NLM + الزاوية NML + الزاوية LNM = 180 ,80 + 90 + الزاوية LNM = 180 الزاوية LNM= 180 – 80 – 90 إذًا الزاوية ل م ع = 20 .
ختاماً تعد خواص الدائرة من أهم الأشكال الهندسية الشهيرة والتي لها استخدامات كثيرة في مجالات الحياة المتنوعة..
أتمنى أن أكون قد قدمت الفائدة العلمية عن خواص الدائرة وكيفي حساب الزوايا المحيطيّة والمركزية والمماسية بأفضل وأسهل طريقة.
لاتنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل لدعمنا والمساهمة في نشر المعلومات والمواضيع الهامة والمفيدة.
دمتم في أمان وطاعة الله والسلام عليكم ورحمة الله وبركاته.
شاهد ايضاً خواص المثلثات وأنواعها وكيفية حساب أطوال المتوسطات والارتفاعات.