
كيفية حساب ميل خط مستقيم ، الخط المستقيم هو مفهوم أساسي في الهندسة الرياضية، ويُعتبر أحد العناصر الأساسية في الجبر والهندسة الرياضية. إذ يُمثل الخط المستقيم مجموعة من النقاط التي تمتد في اتجاه واحد بدون انحناءات. لكن ما يعتبر أحد أهم خصائص الخط المستقيم هو ميله.
الميل هو مقياس للانحدار أو الزاوية التي يأخذها الخط مقارنة بالمحور الأفقي. إنها تُظهر لنا مدى انحدار الخط واتجاهه. عندما نقوم بحساب الميل، نستخدم النقاط على الخط لنحدد الاتجاه والانحدار العام للمسار.
في هذا المقال، سنستعرض الطرق المختلفة لحساب الميل للخط المستقيم، بدايةً من الصيغ الرياضية التقليدية وصولاً إلى استخدام الأدوات التكنولوجية لتسهيل هذا العمل.
سنتعرف في هذا الدرس إن شآءالله عن :
- ما المقصود بميل الخطوط المستقيمة
- تعريف ميل الخط المستقيم مع مقدمة عامة عن المستقيمات والميول
- العلاقة والمعادلة العامة لحساب ميل مستقيم
- أمثلة متنوعة عن حساب ميل الخطوط المستقيمة
- بعض الملاحظات والتحذيرات الهامة
- أهمية حساب ميل المستقيمات في علوم وتخصصات الرياضيات
مقدمة عامة عن المستقيمات ميل خط مستقيم :
علم الرياضيات بجميع فروعه (الجبر والهندسة وغيرها من الفروع والتخصصات ) مليئة بالخطوط والقطع المستقيمة والأضلاع المستقيمة
وسيصبح فهمك للعديد من الأمور الرياضية والفيزيائية جيدًا إذا عرفت كيف تحسب ميل أي خط مستقيم قد يمر معك ويواجهك، ستتعلم خواص المستقيمات وبعض الحالات الخاصة للمستقيمات ، ستعلم أيَضاً متى يكون الخطان أو المستقيمان متوازيان أو متعامدان أو متقاطعان وفي أي نقطة محددة سيتقاطعان أو سيتعامدان ، وأشياء ومعلومات آخرى ..
كيفية حساب ميل أي خط مستقيم بشكل سهل وواضح سوف نتعلم كيفية حساب قيمته بمتابعة الخطوات البسيطة القادمة:
معادلة الميل
افهم معادلة الميل جيدًا :
فميل الخط هو الزيادة داخل المدى Rise أي الفرق بين قيمتي الأكسات X بين نقطتين على الزيادة داخل المجال Run أي فرق الوايات Y لنفس النقطتين أي حاصل قسمة فرق (أي طرح القيمتين ) الأكساتX على فرق الوايات Y
كيفية حل معادلة الميل
ارسم الخط المستقيم الذي تريد حساب ميله:
تأكد أن الخط مستقيمٌ فلا يمكن إيجاد ميل لخط غير مستقيم.
اختر نقطتين على هذا الخط المستقيم وحدد إحداثيات كا من هذه النقطتان حيث الإحداثيات هي القيمة المقابلة على محور السينات أو محور الأكسات “x” وعلى محور الصادات أو محور الوايات “y” يتم كتابتها بالشكل التالي (x, y) أي نكتب قيمة X أولاً ثم قيمة Y
لا يهم أي نقطتين ستختار طالما أنهما نقطتين مختلفتين تقعان على نفس الخط المستقيم أي الشيء الضروري والأساسي أن نختار نقطتين مختلفتان وغير منطبقتان على ذات المستقيم الذي نقوم بدراسته.
حدد أي من النقطتين ستكون النقطة الرئيسية والأساسية في معادلتك:
لا يهم أي النقطتين ستختار طالما أنها ستبقى بلا تغيير أو تبديل طوال حساباتك وحلك للمسألة حيث النقطة الرئيسية الأولى ستكون إحداثياتها x1 وy1
بينما النقطة الأخرى الثانية ستكون إحداثيتها x2 وy2. أي يجب المحافظة على ترتيب النقاط مع الحفاظ على تعويض قيم إحداثيات هذه النقاط بشكل صحيح ..
اكتب المعادلة بشكل واضح وصحيح حيث تكون إحداثيات محور الصادات أو محور الوايات “y” في البسط دوماً أي في بسط الكسر دائماً و إحداثيات محور السينات أو محور الأكسات “x” في المقام دوماً أي في مقام هذا الكسر دائماً ليصبح الكسر على الشكل التالي :
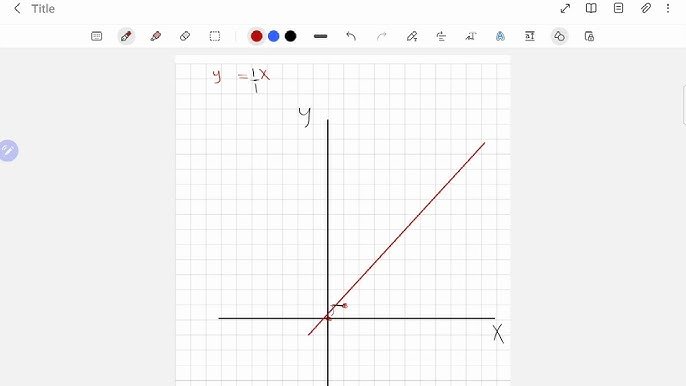
قيمة ميل خط مستقيم X1-X2/Y1-Y2 =
اطرح إحداثيات محور الصادات أي إحداثيات النقاط المختارة على محور الوايات Y من بعضها
اطرح إحداثيات محور السينات أي إحداثيات النقاط على محور الأكسات X من بعضها
قم بتقسيم ناتج طرح إحداثيات محور الأكسات Xعلى ناتج طرح إحداثيات محور الوايات Y
قم بمراجعة الحل للتأكد من أن الناتج منطقي وصحيح
ملاحظات هامة ميل خط مستقيم :
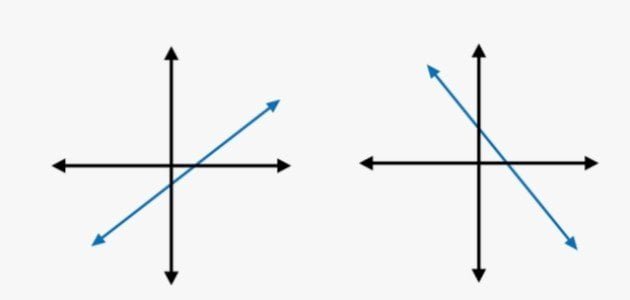
- ميل الخطوط المستقيمة التي تتزايد من اليسار إلى اليمين يكون موجبًا دائمًا حتى لو كان كسورًا عشرية أي إذا كان التزايد في الميل بعكس اتجاه عقارب الساعة فإن الميل يكون موجبًا في هذه الحالة
- ميل الخطوط المستقيمة التي تتناقص من اليسار إلى اليمين يكون سالبًا دائمًا حتى لو كان كسورًا عشرية أي إذا كان التناقص في عكس اتجاه عقارب الساعة يكون الميل سالباً في هذه الحالة
المثال الأول:
المعطيات: الخط المستقيم AB
الإحداثيات: A : (-2, 0) B : (0, -2)
(y2-y1): -2-0=-2; Rise = -2 نقوم بإخراج ناتج طرح الوايات Y
(x2-x1): 0-(-2)=2; Run = 2 نقوم بإخراج ناتج طرح الأكسات X
ميل الخط المستقيم AB = (Rise/Run) = -1
بعض الأفكار المفيدة والهامة :
بعدما تقرر النقطة الرئيسية وهي النقطة الأولى مثلاً لا تقم بتبديلها أو تغييرها أثناء حل المسألة حتى لا تحصل على نتائج وقيم خاطئة وبالتالي تصبح قيمة الميل خاطئة
يتم التعبير عن علاقة أو معادلة ميل خط مستقيم كالتالي:
y=mx+b حيث “y” هي قيمة إحداثيات محور الوايات Y عند نقطة معينة ومحددة و “m” هو ميل هذا الخط المستقيم و”x” هي قيمة إحداثيات محور الأكساتX عند نقطة محددة بينما “b” هي الجزء المقطوع من محور الوايات Y .
بعض التحذيرات الهامة والضرورية في ميل خط مستقيم :
- لا تخلط معادلة ميل خط مستقيم مع أي معادلة أخرى كمعادلة المسافة أو الخط المستقيم أو معادلة القطع المكافئ وغيرها من المعادلات والعلاقات الرياضية…
الأشياء والمعدات البسيطة التي ستحتاج إليها لرسم المستقيمات وحساب الميل :
- ورقة رسم بياني أي ورقة لوغارتيمية أو نصف لوغاريتمية ويمكنك استخدام أي ورقة مقسمة أفقياً وشاقولياً إلى مربعات صغيرة الخاصة بالرسم (إن أمكن)
- مستوى إحداثيات ديكارتي أو خط بنقطتين معروفة قيم إحداثياتهما إو معروفة المسافة بين هاتين النقطتين على الأقل ومن معرفة قيمة المسافة نستطيع حساب قيم الإحداثيات النقاط التي أخترناها أو إيجاد فرق الأكسات والوايات يشكل مباشر سنتعلم على هذه المهارات في الدروس القادمة إن شآءالله..
والتأكد من صحة الحل نأخذ نقطتين غير النقطتان المختارات ونجد الميل بين هاتين النقطتين ويجب أن تكون قيمة الميل موحدة مهما اختلفت قيم إحداثيات النقاط..
يوجد طرق وقوانين وعلاقات متنوعة لحساب ميل الخطوط المستقيمة سنتعرف عليها في الدروس القادمة إن شآءالله
أتمنى أن أكون قد قدمت الفائدة العلمية عن كيفية حساب ميل مستقيم اعتماداً على إحداثيات النقاط بشكل سهل وبسيط
لاتنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل لدعمنا والمساهمة في نشر المعلومات والمواضيع الهامة والمفيدة دمتم في أمان وطاعة الله والسلام عليكم ورحمة الله وبركاته
شاهد ايضاً مفهوم الاستقراء الرياضي واهميته .










