
كيفية حل المعادلة التربيعية هذا الدرس ينتمي لعلم الجبر والمعادلات الخطية .
- سنتعرف في هذا الدرس إن شآءالله عن:
- تعريف المعادلات التربيعية وكثيرات الحدود من الدرجات الثانية
- مقدمة عامة عن المعادلات التربيعية وأهميتها
- كيفية حل المعادلات التربيعية بأفضل وأهم الطرق وأبسطها
- أمثلة متنوعة وشاملة عن المعادلات التربيعية

مقدمة عامة حول حل المعادلة التربيعية مع تعريفها :
يمكن تعريف المعادلة التربيعية : Quadratic equation بأنّها تعبير جبري من الدرجة أو الرتبة الثانية وتكون الصيغة القياسية العامة لمعادلته هي: AX² + BX +C =0 ، حيث:
(A ) هي معاملات أو أمثال X² أي أمثال مربع المجهول و B هي معامل أو أمثال المجهول X و(X ) هو المتغيرأو المجهول في المعادلة ويوجد بدرجتين أو قوتين مختلفتين الأولى من الدرجة الأولى والثانية من الدرجةالثانية ، و(C ) هو الحد المطلق أو الثابت .
ويمثل الحد المعلوم في المعادلة أي يكون عدد لوحده من دون أي مجهول معه ، والشرط الأساسي للحصول على معادلة تربيعية أو من الدرجة الثانية هو أن يكون معامل أو أمثال X² لا يساوي صفر (A ≠ 0)، لأن إذا انعدم الحد A معامل أو أمثال X² .
تصبح المعادلة من الدرجة الأولى أي تتغير درجة المعادلة ويتغير معها حلها لذلك الأمثال يجب لا تكون معدومة ومساوية للصفر ولكتابة المعادلة بشكلها القياسي يتم كتابة الحدAX² أولاً أي في بداية الجملة دوماً متبوعاً بالحد BX ثم كتابة الحد الثابت والمعلوم C وبشكل عام تتم عادة كتابة القيم الرقمية لـ A و B و C على شكل قيم صحيحة غير كسرية أو عشرية كالأعداد ١ ٢ ٤ ٣ ٧ ٨ -١ -٢ -٩ -١١ .

شاهد ايضاً المعادلات من الدرجة الأولى بمجهول واحد : المعادلة البسيطة.
أشهر طرق حل المعادلات التربيعية وكثيرات الحلول مم الدرجة الثانية:
يتم الحصول على حلول المعادلة التربيعية بعدة طرق من أهمها:
- تحليل المعادلة التربيعية إلى العوامل
يمكن حل المعادلة التربيعية عن طريق تحليلها إلى عوامل تعطينا قيم X عند مساواتها بالصفر، وفيما يلي خطوات حل المعادلة التربيعية بالتحليل:
تحويل المعادلة إلى الصيغة القياسية للمعادلة التربيعية التي يكون فيها أحد أطراف المعادلة يساوي صفراً : AX² +BX +C= 0 .
تحليل الطرف غير الصفري (AX² + BX + C ) إلى عوامله الخطية أي جداء عوامل جداء حدين
مساواة كل عامل من العوامل الناتجة بالصفر وإيجاد قيمة X .
مثال: حل المعادلة الآتية: X² – 3X- 10 = 0 باستخدام طريقة التحليل إلى جداء عوامل
نلاحظ أن المعادلة مكتوبة حسب الصيغة القياسية للمعادلة التربيعية، وهي: X²- 3X – 10 = 0.
تحليل الطرف غير الصفري (X² – 3X – 10) إلى عوامله الخطية أي جداء حدين أو قوسين
(X² – 3X – 10) = (X -5)(X +2) = 0.
أي نحاول إيجاد عددين جداءهما يساوي العدد C وهو -١٠
ومجموع هذين العددين يساوي العدد B وهو -٣
نجد أن العددين هما -٥ و ٢ .
مساواة كل عامل من العوامل الناتجة بالصفر وإيجاد قيمة X :
X -5 = 0، ومنها نحصل على قيمة X = 5.
X+2= 0، ومنها نحصل على قيمة X = -2.
قيم X أو مجموعة حلول المعادلة التي تمثل حل المعادلة هي X = (5، -2).
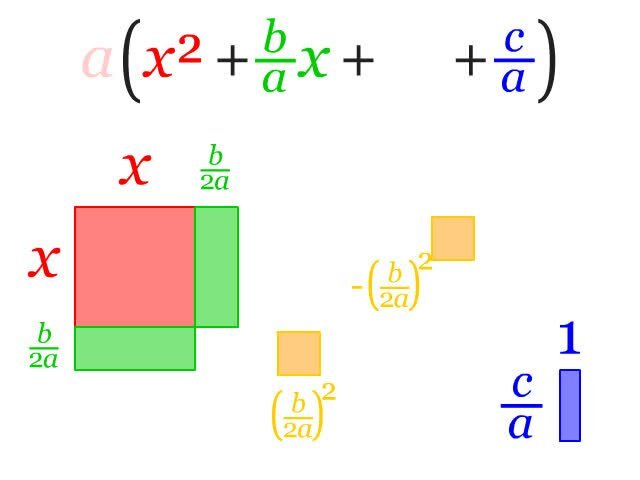
- استخدام إكمال المربع أو الإتمام إلى مربع كامل :
يُستخدم إكمال المربع في حل المعادلة التربيعية أي المعادلات وكثيرات الحدود من الدرجة الثانية ، وفيما يلي خطوات حل المعادلة التربيعية بطريقة إكمال المربع أو الإتمام إلى مربع كامل :
أولاً :قسمة طرفي المعادلة على (A ) أمثال أو معاملات X² لنحصل على المعادلة: X² + (B/A )X + (C/A ) = 0= 0/A أي جعل أمثال أو معامل X² = 1 .
ثانياً :طرح (C/A ) من طرفي المعادلة لتصبح المعادلة : X² + (B/A )X = – (C/A) أي طرح الحد الثابت من المعادلة بعد إجراء التعديلات عليها .
ثالثاً: إضافة ² (B/2A) أي مربع نصف أمثال أو معاملات X (نقسم معاملات X على ٢ ثم نربعها ثم نضفها لطرفي المعادلة أو يمكن آخذ نصف أمثال أو معاملات X مباشرةً وتربيعها وإضافتها لطرفي المعادلة أو إضافتها وطرحها من طرف واحد من المعادلة كل الطرق صحيحة الشيء الهام والضروري هو إبقاء المعادلة متوازنة ومتساوية ) لطرفي المعادلة لنحصل على: X² + (B/A)X + ²(B /2A) = – (C/A) + ²(B/2A) .
الطرف الأيمن للمعادلة. X² + (B/A)X+ ²(B/2A) يمثل “ثلاثي حدود يشكل مربعاً كاملاً” ويمكن كتابته بصورة ²(X+(B/2A)) أي جعله مطابقة شهيرة من الدرجة الثانية ؛ وذلك بوضع بين قوسين جذرX² أي المجهول X وهو يمثل الحد الأول ثم أخذ إشارة الحد الثاني أو الحد الذي يقع في منتصف المعادلة أي إما إشارة موجبة وإما سالبة ± ثم وضع جذر الحد الثالث ²(B /2A) أي (B/2A ) ، والطرف الآخر الأيسر(-(C/A) +²(B/2A)) ناتجه يمثّل عدد ثابت
أخذ الجذر التربيعي لطرفي المعادلة الناتجة لنحصل على جذور المعادلة لتكوين عواملها.
مثال: حل المعادلة الآتية: 5X² – 4 X – 2 = 0
قسمة طرفي المعادلة على العدد (5) لنحصل على X² – (4/5) X – (2/5) = 0.
إضافة (2/5) لطرفي المعادلة لتصبح: X² – (0.8) X = (0.4) .
إضافة (B /2A)2 لطرفي المعادلة والتي قيمتها (-4/ 2×5)2 = 0.16 لنحصل على : X² – (0.8)سX + 0.16 = 0.4 + 0.16 .
الطرف الأيمن للمعادلة: X² – (0.8) X + 0.16يمثل “ثلاثي حدود يشكل مربعاً كاملاً” ويمكن كتابته بصورة ²(X – 0.4) ، والطرف الأيسر مجموعه يساوي 0.56.
- أخذ الجذر التربيعي لطرفي المعادلة لنحصل على: ²(X – 0.4) √ = 0.56√، ومنه: (X – 0.4) = 0.748±
الآن نخرج قيم X لوحدها وهي تمثل حلول المعادلة هي:
الحل الأول للمعادلة نأخذ الإشارة الموجبة : (X – 0.4) = +0.748، ومنه: نخرج X المجهول لوحده ويمثل الحل أو الجذر الأول
X¹ = 1.148
الحل الثاني للمعادلة : (X – 0.4) = – 0.748 نأخذ الإشارة السالبة ونخرج المجهول Xلوحده
X٢ = 0.348-
- استخدام القانون العام للمعادلة التربيعية (قانون المميز أو الدلتا )

يستخدم القانون العام للمعادلة التربيعية في حل المعادلة التربيعية، وفيما يلي صيغة هذا القانون: 4.A.C B² – =D دلتا .
يسمّى المقدار(² B 4A.C -) في الصيغة السابقة بالمميز أوقانون دلتا ، لأنه يمكن أن يميز بين أنواع الإجابات والحلول الممكنة لتحليل المعادلة التربيعية كالتالي :
حلان حقيقيان نحصل عليهما عندما تكون قيمة (B2 – 4.A C) أكبر من صفر (موجبة). أي عندما تكون إشارة D موجبة يكوم للمعادلة جذران أو حلان حقيقيان .
حل حقيقي واحد (كلا الحلين متماثلين ومتساويان ) ونحصل عليه عندما تكون قيمة (2B – 4A .C .) تساوي صفراً.
زوج من الحلول المعقدة أي أعداد عقدية سنتطرق إليها لاحقاً إن شآءالله عندما نتعرف على الأعداد العقدية وطبيعتها وخواصها ، نحصل عليه عندما تكون قيمة (B2 – 4.A.C) أقل من صفر (أي الإجابة سالبة).
مثال: جد حلول المعادلة التربيعية الآتية: 5 X² + 6 X + 1 = 0 باستخدام القانون العام للمعادلة التربيعية.
تحديد قيمة كل من: A= 5 ، B= 6 ، C= 1.
حساب المميزأو دلتا Delta: B² – 4.A.C = ²(6) – (4×5×1) = 16 (قيمة المميز “موجبة”؛ أي أنها معادلة تربيعية لها حلان حقيقيان ).
إيجاد حلول المعادلة باستخدام القانون العام للمعادلة التربيعية:
X= ( -B± جذرD)/ 2A .
لإيجاد الحل الأول نقوم باختيار إشارة جذر الدلتا D الموجبة .
ولإيجاد الحل الثاني نقوم باختيار إشارة جذر الدلتا D السالبة .
، ومنه:
X = (-6 + (16)√) ÷ (2×5) = -0.2.
X= (-6 – (16)√) ÷ (2×5) = -1.
الحلول هي: X¹ = -0.2
X²= -1.
أتمنى أن أكون قد قدمت الفائدة العلمية عن كيفة حل المعادلات التربيعية أو كثيرات الحدود من الدرجة الثانية بأفضل وأهم الطرق وبشكل مبسط إن شآءالله مع ذكر بعض الخواص والأمثلة عليها .
لا تنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل لدعمنا والمساهمة في نشر المعلومات والمواضيع الهامة والمفيدة.
دمتم في أمان وطاعة الرحمن والسلام عليكم ورحمة الله.
شاهد ايضا قواعد الإشارات ( + ـــ × ÷ ) في الرياضيات مع أمثله.










