مفهوم الاستقراء الرياضي واهميته

 الاستقراء الرياضي، هو عبارة عن قراءة المعطيات والأعداد الطبيعية المتسلسلة والمتتالية وراء بعضها البعض

والتحقق من صحة المعطيات أو حساب مجموع هذه الأعداد بطريقة بسيطة من خلال قوانين معينة ..

سنتعرف في هذا المقال إن شآءالله عن :

1.  مفهوم الاستقراء الرياضي : أهمية وفوائد بحث المتتاليات أو الاستقراء الرياضي
2. تفسير الاستقراء الرياضي
3. أستعمالات الأستقراء الرياضي المتنوعة .
4. أمثلة على الاستقراء الرياضي

  تعريف مفهوم الاستقراء الرياضي

الإستقراء الرياضي يعرف  Mathematical induction بأنه مفهوم أو  أسلوب رياضي وتحليلي يتم استخدامه لإثبات النتائج  والتحقق منها ومعرفة مدى صحتها التي يتم الحصول عليها من خلال إثبات الفرضيات والمعادلات  الرياضية التي تكون إما نظرية أو صيغة معينة للأعداد الطبيعة أي …4  ,n = 0, 1, 2, , 3.

حيث يقوم على خطوتين أساسيتين  ورئيستين وهما: إثبات أن العبارة صحيحة للقيمة الأولية التي يتم استخدامها والتي عادة ما تكون ١n = إثبات أن العبارة التي كانت صحيحة عند استخدام القيمة الأولى ستبقى صحيحة وثابتة عند القيام بتعويض رقم طبيعي آخر أي  n = k+1 ؛أو n=k+2   وهكذا ..حيث إن قيمة k هي القيمة التي تم إثباتها حسابها  بالخطوة الأولى في هذه العملية .

 تفسير الاستقراء الرياضي

يتم تشبيه عملية الاستقراء الرياضي بقطع الدومينو أو بلعبة الغولف . إذ أنّ سقوط القطعة الأولى في الدومينو يتسبب بسقوط القطع التي تكون خلفها والتي بدورها تسقط قطع الدومينو الأخرى المتواجدة في الخلف وبالنهاية كل قطع الدومينو سيتم هدمها وتساقطها واحدة تلو واحدة ؛ حيث لا يحدث هذا التأثير إلا بسقوط القطعة الأولى والذي يشبه بذلك ارتباط جميع العناصر بشبكة أو بحبل مثلاً ؛ أن سقط عنصر سحب باقي العناصر معه إذ يشابه مبدأ عمل الاستقراء الرياضي أو بحث المتتاليات .

 خطوات البرهان باستخدام الاستقراء الرياضي؟

ما فائدة الاستقراء الرياضي؟

الاستقراء الرياضي هو عملية استنتاج تستند إلى النماذج الرياضية والتفاضل والتكامل. يتيح الاستقراء الرياضي للرياضيين والعلماء في مجال الرياضيات تحليل وفهم الظواهر الطبيعية والتنبؤ بسلوكها المستقبلي. وفي العديد من الحالات، يمكن استخدام الاستقراء الرياضي لحل مشكلات عملية في مجالات مثل الفيزياء والهندسة والاقتصاد.

من الفوائد الأساسية للاستقراء الرياضي:

1. توضيح العلاقات: يساعد الاستقراء في فهم العلاقات بين متغيرات مختلفة وكيفية تأثير تغير إحداها على الأخرى.
2. التنبؤ: يسمح الاستقراء بتطوير نماذج توضع باستخدام البيانات المتاحة لتنبؤ القيم المستقبلية أو التصرفات المحتملة.
3. تحسين الأداء: يسمح الاستقراء بتحسين أداء النماذج الرياضية وتحسين دقتها في التنبؤ.
4. فهم الظواهر المعقدة: يمكن استخدام الاستقراء لفهم وتحليل الظواهر المعقدة التي تتضمن العديد من المتغيرات والتفاعلات بينها.
5. تطوير التقنيات والتكنولوجيا: يستخدم الاستقراء في تطوير التقنيات والتكنولوجيا في مجالات مثل الاقتصاد الرقمي والتحليل الاحصائي والذكاء الاصطناعي.

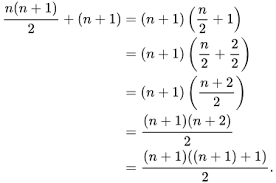
 أمثلة على الاستقراء الرياضي

هذه بعض التمارين و الأمثلة المحلولة على المتتاليات أو السلاسل أو الاستقراء الرياضي: مثال (1): أثبت أن 1 + 3 + 5 +…..+(2n-1) = n)^2 )عندما تكون …. , 3 , 2, n = 1.

 الحل: أثبت أن الجملة صحيحة عندما تكون n = 1 عوض فيها (2n-1) = n^2 2×1-1 = (1)^2 1 = 1 ؛ هذه الجملة صحيحة افرض أن الجملة صحيحة عندما تكون n = k 1 + 3 + 5 +…..+ (2k-1) = k^2 أثبت أن الجملة صحيحة عندما تكون 1+n = k بعد تعويضها 1 + 3 + 5 +…..+ (2k-1) + (2×(k+1) – 1) = k+1)^2) نعوض مكانها لتسهيل الحل حيث تصبح: k^2 + (2 ×(k+1) – 1) = (k+1)^2 k^2 + 2K + 2 – 1 = k^2 + 2k + 1

k^2 + 2K + 1 = k^2 + 2k + 1

بما أن حدّي هذه الجملة متساويان  فتكون بذلك الجملة  محققة وصحيحة.

مثال (2): أثبت أن    a)^n × (b)^n = (ab)^n) لكل الأعداد الطبيعية .

الحل: أثبت أن الجملة صحيحة عندما تكون n = 1 a)^1 × (b)^1 = (ab)^1) ab = ab؛ هذه الجملة صحيحة افترض أن الجملة صحيحة عندما تكون n = k a)^k × (b)^k = (ab)^k) أثبت أن الجملة صحيحة عندما تكون 1+n = k بعد تعويضها (a)^(k+1) × (b)^(k+1) = (ab)^(k+1) بما أنه تم إثبات بالخطوة الأولى أن a)^k × (b)^k = (ab)^k) يمكن استخدامها في الحل حيث أن: (a)^(k) × (b)^(k) × (ab) = (ab)^(k) × (ab)؛ عن طريق ضرب الحدين ب(ab) ومنه ينتج بعد التوزيع: (a)^(k+1) × (b)^(k+1) = (ab)^(k+1)؛ أي أن الجملة صحيحة بتساوي الحدّين.

وفي الختام للاستقراء الرياضي أوبحث المتتاليات والسلاسل دور كبير وهام في علم الرياضيات وفي مجالات الحياة .

أتمنى أن أكون قد قدمت الفائدة العلمية عن المتتاليات والاستقرار الرياضي .

لاتنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل دمتم في أمان وطاعة الله والسلام عليكم ورحمة الله وبركاته

 شاهد ايضاً تعريف علم الرياضيات 2023.