تعد نظرية ذات الحدين وقوانينها من أهم النظريات والقوانين في علم الرياضيات ولها دور كبير في تسهيل العمليات الحسابية إلى حد كبير وتوفير الوقت والجهد بشكل ملحوظ وأول من أوجد هذه النظرية وقام بتطويرها العالم أقليدس.
سنتعرف في هذا المقال عن :
- تعريف نظرية ذات الحدين
- مبدأ نظرية ذات الحدين
- أمثلة على نظرية ذات الحدين
- أهمية وفوائد ذات الحدين
- شرح نظرية ذات الحدين وقوانينها
- قوانين وعلاقات ذات الحدين
- دور القوانين والعلاقات في الحصول على النتائج بدقة عالية مع توفير الوقت والجهد بشكل كبير .
أولاً: تعريف نظرية ذات الحدين والتوافيق :
التعريف بنظرية ذات الحدين تساعد نظرية ذات الحدين بشكل رئيسي في إيجاد القيمة الواسعة والمفصلة لإيجاد أو للتعبير الحسابي و الجبري للصيغة A+ B)ⁿ ) بشكل مفصل إذ إنّه من السهل إيجاد قيمة كلّ من A+B)²، ) و A + B)³، ) A+ B+ C)² ) حيثُ يمكن الحصول على الناتج بضرب مابين القوسين ببعضه بعدة مرات حسب قيمة الأس ٢ أو ٣ أو ⁿ أو عن طريق حلها بطريقة المطابقات .ولكن عندما يصبح الأس عدد كبير أو تصبح الحدود كثيرة هنا يصبح من الصعب جداً حل هذه الحدود وإيجاد الناتج بشكل دقيق ونحتاج إلى آلة حاسبة لحسابها ولكن العلماء أوجدوا قوانين وعلاقات ساعدت في حل المسائل ذات الحدود المعقدة والصعبة من خلال تحويلها لمسائل بسيطة وحلها بطريقة سهلة وبدقة عالية .ونعني بالتعبير ذو الحدين على أنّه تعبير جبري يحتوي على مجهولين أو حدين مختلفين بينهما إشارة جمع أو طرح بالأس ⁿ . مثل:
A+B) (A+B)³ ) ومن الجدير بالذكر أنّه من الصعب إيجاد الصيغة المفصلة للتعبيرات ذات الحدود الأسيّة العالية بنفس الطريقة المشروحة سابقاً ، لأنّه سيكون مملاً ويستغرق جهداً ووقتاً طويلاً، ولكن يمكننا إيجادها بمساعدة نظرية ذات الحدين، والتي تسمح لنا بإيجاد A + B) ⁿ ) دون ضرب ذات الحدين في نفسه n مرات حيث ساعد هذا القانون بتوفير الوقت والجهد إلى حد كبير.
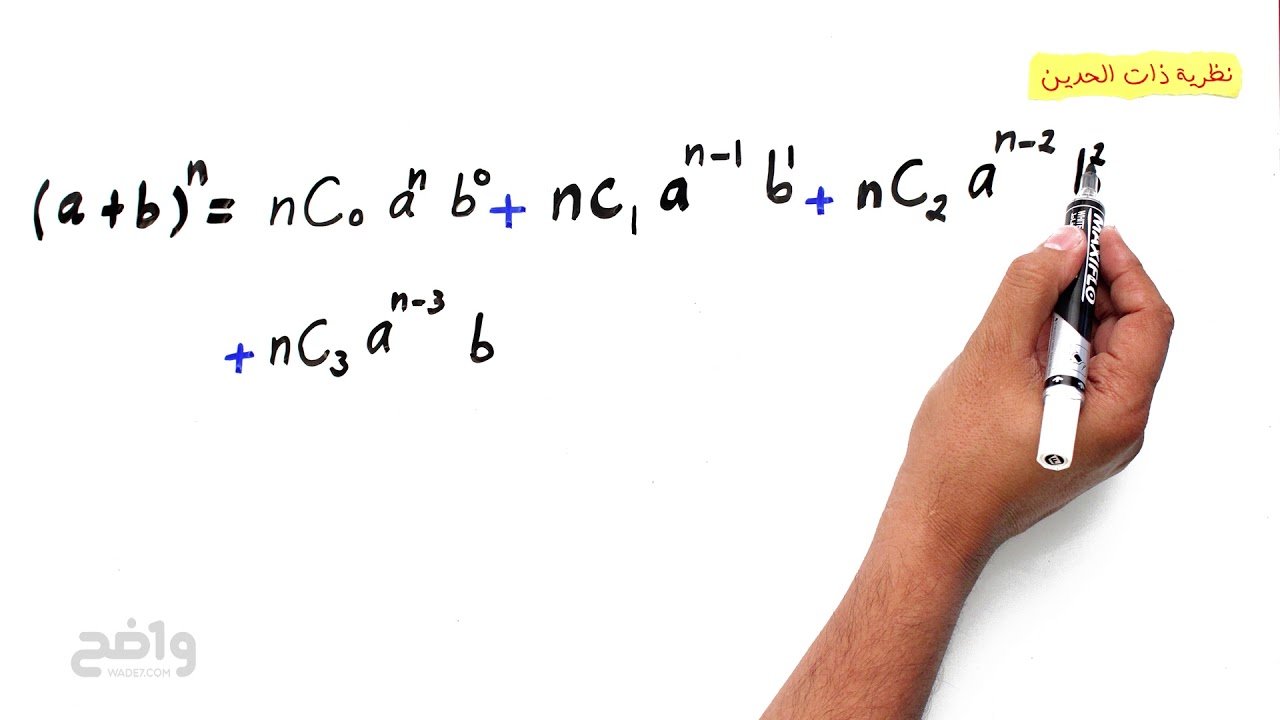
ثانياً : مبدأ نظرية ذات الحدين
وجدت نظرية وقوانين ذات الحدين في القرن الرابع قبل الميلاد من قبل العالم اليوناني المشهور باسم إقليدس، إذ تنص على مبدأ تفصيل التعبير الحسابي و الجبريّ
A+ B)) وتُعبر عنه كمجموع للحدود التي تتضمن الأسس الفرديّة للمتغيرات Aو B حيثُ يرتبط كلّ حد في التوسُّع ذي الحدين بقيمة ثابتة تسمى الأمثال أو المعامل.

شاهد ايضاً كيفية حساب النسبة المئوية بأفضل و أسهل طريقة
ثالثاً:نص نظرية ذات الحدين
تنص نظرية ذات الحدين على مصطلحين هامين وأساسيين ، وهما: المعامل ذي الحدين، والتوسُّع ذي الحدين، سنشرحها في الفقرات الآتية :
توضيح التوسع ذي الحدين بالمثال التالي :
A + B)ⁿ = ∑ C (n,k) (A(n-k)) (Bk) =)
An + C (n,1) (A(n − 1)) B + C (n,2) (A(n − 2)) (B2) + .
.. + C (n,n-1) x (B(n − 1)) + Bn

رابعاً: أمثلة على نظرية ذات الحدين
يُمكن الاطلاع على الأمثلة التوضيحيّة الآتية على كلّ من المعامل ذي الحدين والتوسع ذي الحدين:
مثال 1: جد المعامل ذي الحدين لـ C (4,2)
. الحل: C (n,r) = n! / (r! (n − r)!)
C (4,2) = 4! / (2! (4− 2)!) = (4×3×2!) / (2!x2!)= 12 / 2=6
مثال 2: جد المعامل ذي الحدين لـ
C (5,3)
الحل: C (n,r) = n! / (r! (n − r)!)
(5,3) = 5! / (3! (5 − 3)!)= (5x4x3!) / (3!x2!)
= 10
مثال 3: جد المعامل ذي الحدين لـ C (6,2).
الحل: C (n,r) = n! / (r! (n − r)!)
C (6,2) = 6! / (2! (6 − 2)!)= (6x5x4!) / (4!x2!) = 30/ 2= 15
أتمنى أن أكون قد قدمت الفائدة العلمية عن نظرية ذات الحدين بشكل مفصل وبسيط
لاتنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل لدعمنا والمساهمة في نشر المعلومات الهامة والمفيدة.دمتم في أمان وطاعة الله والسلام عليكم ورحمة الله وبركاته ♥️
شاهد ايضاً خواص المثلثات وأنواعها وكيفية حساب أطوال المتوسطات والارتفاعات.