
شرح الجذر التربيعي للعدد الموجب 2023
الجذر التربيعي للعدد الموجبه و عدد مربعه يساوي a
(عملية التربيع معاكسة للجذر كعملية الضرب والقسمة والجمع والطرح واللوغاريتم والأسس …..)
وفي حالة aعدد موجب غير معدوم (أكبر تماماً من الصفر )
يكون للعدد a جذران تربيعيان أحده
سنتحدث في هذا البحث عن الجذور وأنواعها وأهميتها ونشرح إن شآءالله الجذر التربيعي بالتفصيل 
تعريف الجذر التربيعي :
الجذر التربيعي لعدد موجب a ما موجب نرمز إليه بالرمز + جذرa والجذر التربيعي الآخر سالب ويرمز له بالرمز -جذر a
أما في حالة a=0 فيكون جذر 0 = 0 ويقرأ الجذر التربيعي للعدد a
عملية تربيع العدد هي رفع الأس من الدرجة الأولى إلى الدرجة الثانية
(ضعف الأس دوماً ) بينما الجذر عملية عكسية للتربيع
فإذا كان العدد بالأس 2 يتحول إلى الأس ١
تتحول الدرجة من الدرجة الثانية إلى الأولى
- وإذا كان العدد بالأس ٤ يتحول الأس إلى ٢
- ( بمعنى أنه يتحول الأس إلى النصف دوماً )
فإن كان الأس واحد يتحول إلى النصف
لذلك جذر أي عدد أو تابع هو العدد والتابع ذاته لكن بالأس نصف ٢/١.
½
مثال جذر العدد ٣ هو ٣
أي أننا قسمنا الأس واحد على ٢ دومأً نقسم الأس على ٢ لنحصل على نصفه وهكذا…..
عندما يطلب مننا حساب جذر أي عدد نحاول أن نجد عدد إذا ضربنا بنفسه نتج العدد الذي تحت الجذر
مثال
جذر إل ٢٥ هو ٥ لان ٥×٥= ٢٥
وجذر إل ٣٦ هو ٦ لأن ٦×٦ = ٣٦
وجذر ٨١ هو ٩ لأن ٩ ×٩=٨١
وإن لم نستطيع إيجاد عدد جداءه بنفسه هو العدد تحت الجذر
نحاول إيجاد عددين جداءهما العدد الذي تحت الجذر
بشرط أن يكون عدد من العددين يمكن جذره بمعنى إذا ضربنا جذره بنفسه نتج أحد العددين
مثال جذر إل ٤٨ هو جذر جداء العددين ١٦ ×٣
نجد أن جذر العدد ١٦ هو ٤ فأصبح الناتج ٤ جذر ال٣ وهكذا…
من خواص الجذور التربيعية
١ جداء جذرين هو جذر الجداء
مثلاً جذر ٣ × جذر٢ هو جذر إل ٣×٢ = ويساوي جذر إل ٦
والعكس صحيح
جذر جداء عددين هو جداء جذور الأعداد ببعضها
جذر (٥×٦) = جذر ٥ × جذر٦ وهكذا…
والقسمة أيضاً تتبع نفس القاعدة
حاصل قسمة جذرين = جذر حاصل قسمة العددين
جذر ١٢ ÷ جذر ٦ = جذر( ١٢÷ ٦ )= جذر ٢
والعكس صحيح
جذر ( ٣٠ ÷١٥ )= جذر ٣٠ ÷ جذر ١٥ = جذر ٢
علماً أن القاعدين السابقتين خاصة فقط بعمليات الضرب والقسمة
ولاتطبق على عمليتي الجمع والطرح
فمثلاً : جذر ١ + جذر٤ لا يساوي جذر (١+٤)
وجذر ٥ – جذر٤ لايساوي جذر(٥-٤) …
فإذا أردنا جمع أو طرح الجذور يجب علينا توحيد الجذور
(نحاول أن نجعل الجذور متشابهة بأي طريقة كانت ثم نجمع الأمثال ونضربها بالجذر … )

ملاحظة هامة
لتحويل الجذور نحاول أن نحلل العدد الموجود تحت الجذر إلى جداء عددين على أن يكون أحد العددين قابل للجذر
وتستخدم من أجل جعل الجذور متشابهة لجمعها أو طرحها
مثال جذر ٢٤ + جذر ٦
نلاحظ أن إل ٢٤ يمكن تحليلها إلى ٦ × ٤ يصبح لدينا تحت الجذر ٤×٦ ومن القاعدة السابقة نحلل جذر الجداء إلى جداء جذرين
جذر ٢٤ = جذر ٦ × جذر ٤ ، جذر ٤= ٢
= جذر ٦ × ٢ =٢ جذر إل ٦
أصبح لدينا ٢ جذر ٦ + ١ جذر ٦. أصبحت الجذور متشابهة نقوم بجمعها = ٣ جذر ال٦
وكذلك عملية الطرح أيضاً
جذر ١٨ – جذر ٢ = ؟
نقوم أولاً بتحويل العدد 18 إلى ٢×٩ يصبح جذر١٨ =جذر ٢ × جذر ٩ ، جذر ٩ = ٣
يصبح جذر ١٨ =٣جذر ٢
تصبح المعادلة
٣ جذر ٢ – جذر ٢ = ٢ جذر ٢
مثال آخر ٥ جذر ٣ + ٦ جذر ٧ – جذر ١٢ – جذر ٧
نقوم بجمع الجذور المتشابهة وطرح الجذور المتشابهة الأخرى
جذر ١٢ = ٢ جذر ٣
تصبح المعادلة من الشكل
٥ جذر ٣ + ٦ جذر ٧ – ٢جذر ٣ – جذر ٧
٣ جذر ٣ + ٦ جذر ٧
مثال جذر ١٢ ÷ جذر ٣ نحلل جذر ١٢ = ٢ جذر ٣ نختصر جذر ٣ من البسط والمقام
يصبح الناتج ٢
مثال. جذر ٣ / (جذر ٣ + جذر ٦ )
بما إن العملية في البسط عملية جمع فنقوم بتقسيم كل جذر على المقام المشترك جذر ٣
يصبح لدينا: جذر٣ / جذر ٣ =١ ؛ و جذر ٦ / جذر ٣ = جذر ٢/١ = (جذر٢ )/١
مثال اكتب العدد (جذر٣) /٢ بصيغة كسر مقامه عدد صحيح
نلاحظ أن المقام هو جذر وتحويله لعدد صحيح (نذكر أن الأعداد الصحيحة هي الأعداد التي لاتحوي على أعداد عشرية تتكون فقط من جزء واحد هو الجزء الصحيح مثل ١ ،٢،٣،-٤،-٥،-٨،…..)
لابد من ضرب البسط والمقام بالجذر ٣.
لكي نستطيع أن نطبق القاعدة : جذر a × جذر a = جذر a مربع
ونحن نعلم أن التربيع يحذف الجذر فأصبح قيمة جداء الجذرين هو قيمة مت تحت الجذر = a
إذاً نضرب البسط والمقام ب جذر ٣ ليصبح المقام جذر٣ × جذر٣= ٣ وهو عدد صحيح موجب…
فأصبح الكسر بالشكل ٣ /( ٢ جذر٣)

مثال آخر
اكتب العدد جذر ٧٢ بصيغة a × جذر b حيث
a و b عددان طبيعيان ( عددان صحيحان موجبان )
الحل
١ نستعرض المربعات التي تصغر العدد ٧٢
٤= ٢² ٣² =٩ ٤² = ١٦ ٥² = ٢٥ ٦² = ٣٦. ٧² = ٤٩ ٨² = ٦٤
٢ نختار منها قواسم العدد ٧٢
٤= ٢² ٣² =٩ ٤² = ١٦ ٦² = ٣٦
٣ نكتب العدد ٧٢ بصيغة a² × b = 72
حيث a² هو أكبر الأعداد الواردة في ٢
٧٢= ٢× ٣٦ = ٦² × ٢ نقوم بجذر العدد ٧٢ = جذر ( ٢×٦²)=
نقوم بتوزيع الجذر على العددين يصبح جذر ٢ × جذر ٦² = جذر٢ × ٦ = ويقرأ ٦ جذر ٢
من أهمية الجذور وفوائدها هي تحويل الأعداد من شكل معقد إلى شكل بسيط
فمثلاً إن كان لدين جداء عددين كبيرين ولم نكن نملك آلة حاسبة نقوم بجذر جداء العددين ثم تربيع قيمة الناتج
فمثلا ٣٦ × ٨١ نقوم بجذر هذا الجداء ليصبح ٦ × ٩ = ٥٤ ثم نربعه = ٢٩١٦
مثال آخر ٩ × ٢٥ نقوم بجذر الجداء = ٣ ×٥ = ١٥
نربع الناتج ١٥ ² = ٢٢٥

ولتسهيل عملية القسمة أيضاً نتبع نفس الأسلوب السابق نقوم بجذر البسط والمقام ثم نربع ناتج القسمة
مثال ٣٦/ ١٤٤ لايمكن قسمته مباشرةً لذلك نجذر البسط والمقام معاً ثم تربيع الناتج لكي لاتتغير قيمة الكسر
يصبح لدينا ٦/١٢ = ٢ نربع الناتج =٤
والحصول على نتائج مجهولة بعمليات معلومة فمثلاً أعطيت مساحة المربع
وطلب مننا حساب طول ضلع ذلك المربع فنقوم بجذر المساحة لينتج طول الضلع
لأن مساحة المربع هي مربع طول الضلع فإذا جذرنا المساحة حذف التربيع وبقي طول الضلع
مثال لدينا أرض زراعية مربعة مساحتها ١٠٠ متر مربع المطلوب حساب طول ضلع هذه الأرض
نقوم بجذر المساحة : جذر ١٠٠ = ١٠ متر
لاحظ أن واحدة المساحة كانت متر مربع قبل أن نجذرها وبعد جذرها أصبحت متر
( حذف المربع (التربييع ) من الواحدة بسبب الجذر )
وكذلك إذا أعطيت مساحة الدائرة نستطيع حساب نصف قطر هذه الأرض
بجذر المساحة وتقسيمها على جذر إل ٣،١٤ …
وكذلك الحجم والمجسمات يمكن حساب مساحة أو طول باستخدام الجذر التربيعي والجذر التكعيبي
الجذر التكعيبي يقوم بجذر العدد مرتين تربيعياً
مثال جذر التكعيبي ٨١ = ٣
بدلاً من جذر العدد مرتين تربيعياً نستطيع جذره مرة واحدة تكعيبياً
أتمنى أن أكون قد قدمت الفائدة العلمية
والله وليُ التوفيق



الجذر التربيعي للعدد الموجب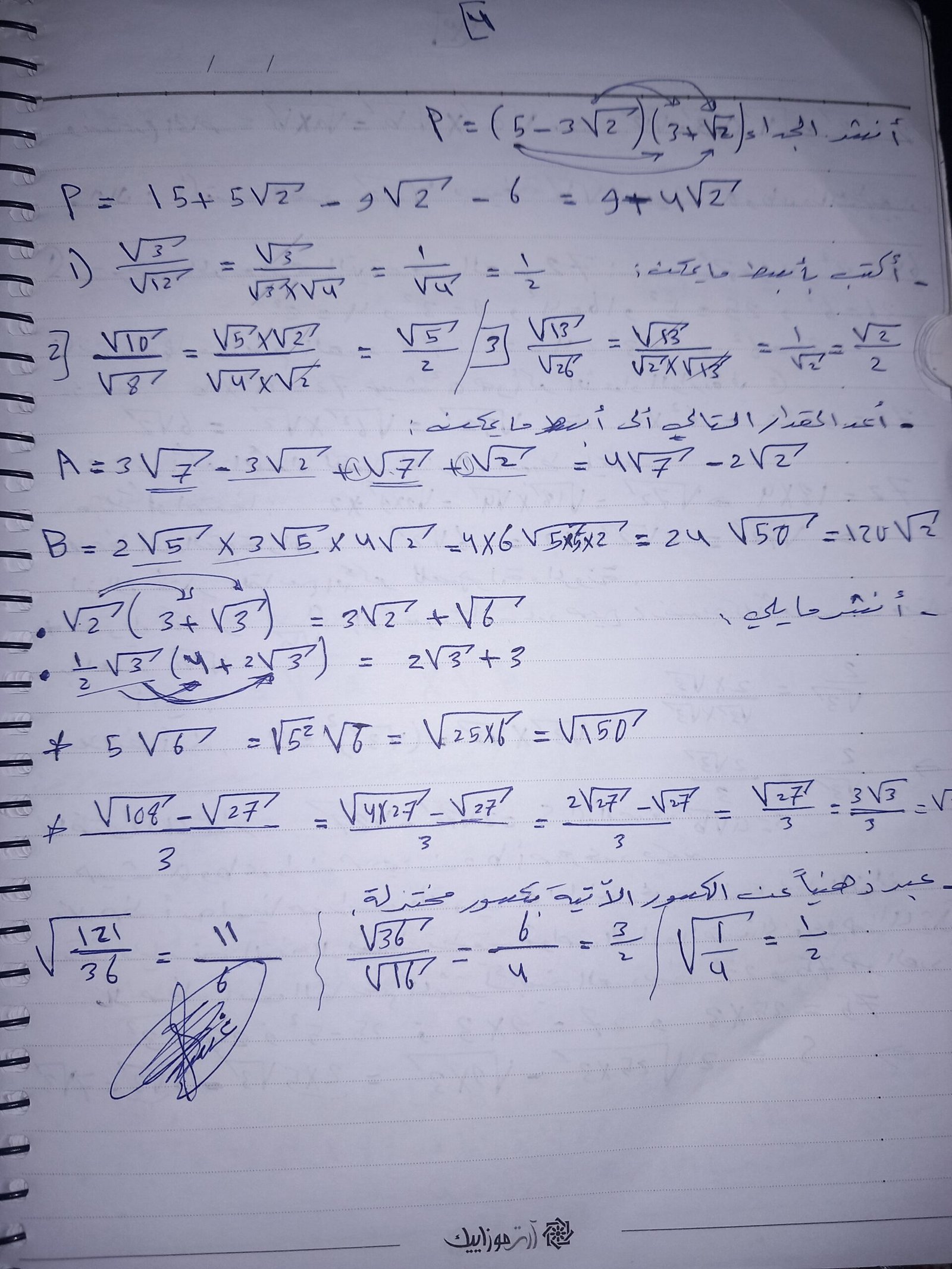



لتحميل ملف الجذر التربيعي للعدد الموجب








