خواص المثلثات وأنواعها وكيفية حساب أطوال المتوسطات والارتفاعات

خواص المثلثات وأنواعها وأستخداماتها وكيفية حساب أطوال المتوسطات والارتفاعات

ماذا يفيد شكل المثلث وما أستخدامااته الشهيرة في الحياة ؟

ماهي خواص المثلثات بحسب أنواعها العديدة ؟

لماذا يلجأ المهندسون والمصممون والحدادون إلى شكل المثلث في كثير من أعمالهم المختلفة ؟

لماذا تصمم الأنابيب والقنوات على شكل دائرة أو على شكل مثلث ؟

هل يمكن حساب زوايا مثلث كن خلال معرفة أطوال أضلاعه أو أطوال المتوسطات ؟ سنقوم بالإجابة عن كل الأسئلة وسنتعرف في هذا المقال إن شآءالله عن :

محتويات المقالة

خواص المثلثات

استخدامات المثلثات في مجالات الحياة

خواص المثلث قائم الزاوية

أهمية الأشكال الهندسية في الهندسة وخصوصاً المثلث

خواص المثلث متساوي الأضلاع

قدرة تحمل المعدات والأنابيب وغيرها عندما تصمم على شكل مثلث أو أجزاء هذه الأشكال تأخذ شكل المثلثات ..

خواص المثلث متساوي الساقين

خواص المتوسطات في المثلث وكيفية حسابها بأبسط طريقة ممكنة

خواص المثلث مختلف الأضلاع

التعرف على متى يكون المتوسط هو ذاته الارتفاع في مثلث محدد

أمثلة متنوعة على أستخدامات وخواص المثلث

التعرف على أهمية المثلثات وأستعمالتها الشهيرة .
كيفية حساب زوايا مثلث بمعرفة أطوال الأضلاع
كيفية حساب أطوال الأضلاع والمتوسطات والارتفاعات في المثلث

مقدمة عامة خواص المثلثات

خواص المثلثات ، يعد المثلث من أهم الأشكال الهندسية الكثيرة والمتنوعة على الأطلاق ولايقتصر أستخدامه في علم الرياضيات فله عدة أستخدامات متنوعة ؛ يستخدم كثيراً في مجالات الحياة وفي كثير من العلوم والاختصاصات المتنوعة بسبب شكله الجميل والمناسب ولأن أيعد من أصغر الأشكال الهندسية من حيث عدد الأضلاع والزوايا لذلك من السهل تصميمه واستخدامه بدلاً من كثير من الأشكال الهندسية الشهيرة والغير شهيرة

من أستخداماته يستخدم في علم الطبوغرافيا لتقسيم الأرض إلى أقسام متساوية ومتناسقة مع بعضها البعض وبسبب أنه يمكن تشكيل الكثير من الأشكال الهندسية من خلا المثلثات فمن خلا مثلثان قائمان نشكل مربع أو مستطيل ومن مثلثان متساويان في أطوال الأضلاع معين ويستخدم في تصميم المنشآت والأنابيب والجوائز والكثير من الاستخدامات الهندسية بسبب تحمله الكبير للضغوط والإجهادات والقوى المختلفة وقلة الزوايا فيه لأنها تشكل نقاط ضعف و ولديه ميزة أنه إذا تعرض ضلع من أضلاع المثلث لقوى كبيرة أو إجهاد أو ضغط يسندانه ويدعمانه الضلعين الآخرين…

أولاً: تعريف المثلث ( Triangle)

هو عيارة عن شكل هندسي أو مُضّلع يتكون من ثلاثة أضلاع أو ثلاث خطوط ، وثلاث زوايا، وثلاث رؤوس حيث الرأس يتشكل من التقاء خطين أو ضلعين ، ويُمكن تلخيص أهمّ خواص المُثلث العامّة على النحو الآتي: مجموع زوايا المُثلث الثلاثة = 180 درجة.. مجموع طول أيّ ضلعين من أضلاع المُثلث أكبر من طول الضلع الثالث.أي أن مجموع طولي أقصر ضلعين في مثلث أكبرمن طول الضلع الثالث

الفرق بين طول أيّ ضلعين من أضلاع المُثلث أقلّ من طول الضلع الثالث أي قرق الطول بين الضلع الأكبرفي المثلث وأصغر ضلع في المثلث =أصغر من طول الضلع الثالث .. الضلع المُقابل للزاوية الكبرى في المُثلث هو الضلع الأطول دوماً ، الزاوية الخارجية للمثلث تساوي مجموع الزاويتين الداخليّتين البعيدتين أي إن الزاوية الخارجية في المثلث تساوي قيمتها مجموع الزاويتين الآخرتين لأن مجموع زوايا المثلث ١٨٠ درجة ومجموع أي زاويتان الخارجية والداخلية في المثلث تساوي ١٨٠ درجة شريطة أن تكون الزاويتان الداخلية والخارجية متجاورتان (في جانب بعضهما البعض ..)، وتُعرف هذه الخاصة باسم (خاصة الزاوية الخارجية).

يتشابه المثلثان ويتطابقان إذا كانت الزوايا المتقابلة لكل من المثلثين مُتطابقة ومتساوية وأطوال أضلاعهما متساوية أو مُتناسبة أي إن نسبة كل ضلع من المثلث الأول على الضلع المقابل له في المثلث الآخر نسبة ثابتة

مثل ٢/١أو ٣أ/١ وهكذا لذلك تسمى بالمتناسبة، قانون مساحة المثلث ومحيط المثلث هما على النحو الآتي: مساحة المثلث= ½× طول القاعدة×طول الارتفاع. محيط المثلث =مجموع جميع أضلاعه الثلاثة وإذا كان المثلث متساوي الأضلاع نضرب طول أي ضلع ب٣ لأن الأضلاع جميعها متساوية ..

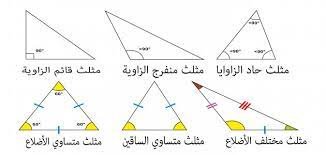
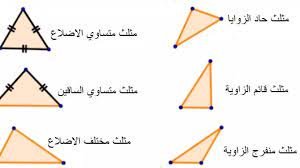
ثانياً: أنواع وتصنيف المثلثات حسب قيم الزوايا :

خواص المثلثات يُعرف المُثلث الذي يكون قياس جميع زواياه أقل من 90 درجة أي كل زاوية قيمتها أقل من ٩٠ درجة وتسمى حادة بالمُثلث حادّ الزوايا ، يُعرف المُثلث الذي يمتلك زاوية واحدة قياسها أكبر من 90 درجة بالمُثلث مُنفرج الزاوية لأننا نعلم أن الزاوية التي قياسها أكبر من ٩٠درجة بالزاوية المنفرجة لذلك يسمى المثلث بالمثلث منفرج الزاوية ، خصائص متوسط المثلث يُعرف خطّ المتوسط للمُثلث على أنّه الخطّ أو القطعة المستقيمة المُمتد من إحدى الزوايا الداخلية إلى مُنتصف الضلع الذي يقابل هذه الزاوية ، وللخط المتوسط عدّة خصائص وخواص منها : يُنصّف المتوسط زاوية الرأس المحصورة بين ضلعين متساويين أي في المثلث متساوي الساقين ومتساوي الأضلاع.. إلى زاويتين متساويتين تماماً في كلٍّ من المثلث متساوي الساقين والمثلث متساوي الأضلاع

ثالثاً: خواص المثلثات :

خواص المثلثات يمتلك المثلث 3 خطوط متوسطة أو ثلاثة متوسطات تتقاطع في نقطة تُسمّى مركز ثقل المثلث أو مركز التوازن الهندسي أو النقطة المركزيّة : Centroid تقسم كل متوسط من المتوسطات الثلاث بنسبة 2:1 أي تقسم كل متوسط لجزئين الجزء الصغير يساوي ثلث طول المتوسط والجزء الآخر يساوي إلى ثلثين طول المتوسط أي إذا نسبنا طول الجزء الصغير في المتوسط على طول الجزء الكبير فإن النسبة هي ٢/١ نصف..
يُنصّف كل متوسط المثلث إلى مثلثين متساويين بقيمة المساحة ويمكن أن يتطابق المثلثان ويمكن إلا يتطابقان . يُمكن حساب طول المتوسط عن طريق نظرية أبولونيوس : متوسط الضلع أ مثلاً : يصبح مع الأختصار الرمز التالي :م أ=( (2بَ²+2جَ²-أَ²) ÷4)√، أو متوسط الضلع ب : م ب=((2أَ²+2 جَ² – بَ²)÷4)√، أومتوسط الضلع ج م ج=(2بَ²+2أَ²-جَ²)÷4)√؛ حيث: م أ: طول خط المتوسط أو القطعة المستقيمة النازلة من الرأس أ،
أَ: طول الضلع المقابل للرأس أ. م ب: طول خط المتوسط أو القطعة المستقيمة النازلة من الرأس ب، بَ: طول الضلع المقابل للرأس ب. م ج: طول خط المتوسط أو القطعة المستقيمة النازلة من الرأس ج، جَ: طول الضلع المقابل للرأس ج.

خواص ارتفاع المثلث يُعرّف الارتفاع Altitude على أّنه القطعة المستقيمة العمودي الممتدة من رأس المثلث إلى الضلع المقابل له وعمودية عليه أي أن الارتفاع مع القاعدة يشكلان زاوية ٩٠ درجة حيث القاعدة هي دوماً تقابل رأس المثلث .

وللارتفاع عدّة خواص منها ما يأتي: ارتفاع المثلث قد يقع داخله أو خارجه أي يمكن أن يكون أرتفاع مثلث ما خارج هذا المثلث ..
لكل مثلث 3 ارتفاعات ، الارتفاعات ممتدة من كل رأس. الارتفاع هو أقصر مسافة من الرأس إلى الضلع المقابل له في المثلث نأخذ دائماً ارتفاع المثلث أقصر مسافة من الرأس إلى القاعدة ونلاحظ أن الزاوية المشكلة قائمة
تلتقي الارتفاعات الثلاثة دائماً في نقطة واحدة بغض النظر عن شكل المثلث تُسمّى بملتقى الارتفاعات
خواص المثلث قائم الزاوية يُمكن تعريف المثلث قائم الزاوية على أنه المثلث الذي يمتلك زاوية قائمة قياسها 90 درجة، وتكون باقي زواياه حادّة حصراً لأن مجموع الزوايا ١٨٠درجة وأحد الزوايا ٩٠ درجة يبقى ٩٠ درجة للزاويتان فحصراً الزاويتان حادتان ، ويُسمّى الضلع المقابل للزاوية القائمة بالوتر وهو أطول ضلع في المثلث، ويُمكن حساب طوله باستخدام نظرية فيثاغورس، حيث يساوي مربع طول الوتر مجموع مربع كل ضلع من أضلاع المثلث الأخرى: (الوتر)²=(الضلع الأول)²+ (الضلع الثاني)²، وبالرموز: أ²=ب²+ج²؛ حيث: أ: طول وتر المثلث قائم الزاوية أي الضلع المقابل للزاوية القائمة .. ب و ج: أطوال أضلاع المثلث قائم الزاوية الأخرى أي الضلعين المتعامدين اللذان يشكلان زاوية قائمة بينهما .. وللمثلث قائم الزاوية عدّة خواص يُمكن تلخيصها على النحو الآتي: يُمكن أن يكون المثلث قائم الزاوية متساوي الساقين إذا تساوى طول الضلعين اللذين يحصران الزاوية القائمة بينهما وبالتالي يصبح قيمة الزاويتان الباقيتان ٤٥ درجة أي الزاويتان متساويتان ..

ملاحظة هامة: لا يُمكن للمثلث قائم الزاوية أن يكون متساوي الأضلاع أبداً ولا بشكل من الأشكال ؛ لأن طول الوتر دائماً أكبر من أطوال الأضلاع الأخرى في المثلث القائم.. المتوسط الممتد من الرأس الذي يحتوي الزاوية القائمة إلى وتر المثلث قائم الزاوية يقسم المثلث إلى مثلثين متطابقين يكون كلّ منها مثلث قائم متساوي الساقين دوماً ويقسم الزاوية القائمة إلى قسمان متساويان أيضاً ، كب منها ٤٥ درجة ..

قاعدة هامة جداً: يكون طول المتوسط المرسوم من الزاوية القائمة مساوياً لطول نصف الوتر دوماً ..يملك المثلث قائم الزاوية ومتساوي الساقين زاوية قائمة وزاويتين حادّتين قياس كلّ منهما 45 درجة، ويكون طول الضلعين الآخرين فيه متساوياً أي عندما نعلم أن المثلث متساوي الساقين أو فيه زاويتان متساويتان نعلم إن فيه ضلعان متساويان وبسبب تساوي ضلعان فيه فإن الزاويتان المرتبطتان بهذان الضلعان أيضاً متساوية .

يمتلك المثلث قائم الزاوية ومختلف الأضلاع أي كل ضلع يختلف بالطول عن الضلع الآخر .. يحتوي زاوية قائمة وزاويتين حادّتين قياس كلّ منهما مختلف عن الآخر دوماً أي مستحيل أن يكون قياس الزوايا ٤٥ درجة ، وتكون أطوال الأضلاع مختلفة أيضاً لنفس السبب والعكس صحيح.

يُمكن تعريف المثلث متساوي الأضلاعEquilateral triangle على أنه المثلث الذي تكون أضلاعه الثلاثة متساوية في الطول ومتطابقة ، وبالتالي ينتج أن جميع زواياه الداخليّة أيضاً متساوية في القياس ومتطابقة ، ويبلغ قياس كلّ منها 60 درجة دائماً.

وللمثلث متساوي الأضلاع عدّة خواص منها: يكون كلّ من الارتفاع وخط المتوسط أو طول المتوسط ومُنصّف الزاوية والمُنصّف العمودي لكل ضلع من الأضلاع أي القطعة المستقيمة التي تعامد الضلع في منتصفه تماماً وكل زاوية من الزوايا هو الضلع أو القطعة المستقيمة نفسها، ويكون طولها متساوياً لجميع الأضلاع، ويساوي: (3√×س)÷2؛ حيث س: طول أي ضلع من أضلاع المثلث متساوي الأضلاع، وعليه تكون أطوال المتوسطات الثلاثة في المثلث متساوي الأضلاع دائماً متساوية .

يُمكن تعريف المثلث متساوي الساقين Isosceles triangle على أنه مثلث يتساوى فيه طول ضلعين من أضلاعه، ويختلف الضلع الثالث في الطول عنهما، ويكون قياس الزاويتين المقابلتين للأضلاع المتساوية في الطول متساوياً في القياس وتسمى زوايا القاعدة،وللمثلث متساوي الساقين عدّة خواص يُمكن تلخيصها كالتالي : تكون قاعدة المثلث متساوي الساقين هي الضلع الثالث الذي لا يساوي طوله طول الضلعيين الآخرين دائماً

خواص المثلثات ، يُنصّف الارتفاع المُمتد من رأس المثلث متساوي الساقين القاعدة إلى قسمين متطابقين و متساويين، و يُنصّف زاوية الرأس إلى قسمين متساويين أيضاً، و يُنصّف الارتفاع المُمتد من رأس المثلث متساوي الساقين المثلث إلى مثلثين متطابقين ومتساووين قائمي الزاوية.. الارتفاع في المثلث متساوي الساقين هو نفسه الخط المتوسط الذي يتوسط القاعدة ويصنع زاوية قائمة مع القاعدة لذلك هو ارتفاع ومتوسط في المثلث يتساوى طول المتوسطات المرسومة من الزوايا المتساوية دائماً في المثلث متساوي الساقين لأن الزاويتان متساويتان فيبعدان نفس البعد عن الضلع المقابل لهذان الزاويتان.

خصائص المثلث مختلف الأضلاع يُمكن تعريف المثلث مختلف الأضلاع Scalene triangle على أنه مثلث تختلف أطوال أضلاعه الثلاثة وقياس زواياه عن بعضها البعض ولا يمكن تساوي أي عنصرين من عناصر المثلث ؛ كلها مختلفة عن بعضها البعض .

وللمثلث مختلف الزوايا والأضلاع : عدّة خواص يُمكن تلخيصها كالآتي : لا يمتلك المثلث مختلف الأضلاع والزوايا أضلاعاً متساويةً في الطول نهائياً . أيضاً لا يمتلك المثلث مختلف الأضلاع زوايا متساوية في القياس أبداً

يُمكن أن تكون زوايا المثلث مختلف الأضلاع حادّة أو منفرجة أو قائمة..كل الاحتمالات واردة
لا يمتلك المثلث مختلف الأضلاع خط تناظر أي لايمكن تقسيمه لقسمين متطابقين نهائياً لأن الأضلاع مختلفة الأطوال والزوايا علماً أن خط المناظر يمر من مركز الثقل للشكل الهندسي فلو طبقنا ذلك على المثلث مختلف الأضلاع لايمكن أن يتطابق الجزئين أبداً ولابحالة من الحالات .
لا يمتلك المثلث مختلف الأضلاع نقطة تماثل. تكون أطوال المتوسطات الثلاثة في المثلث مختلف الأضلاع مختلفة دوماً ويعود السبب لأن أطوال المثلث مختلفة فهذا يؤدي لاختلاف كل عناصر المثلث .

رابعاً: أمثلة متنوعة وعديدة على خواص المثلثات

المثال الأول: إذا كان المثلث ABC مثلث قائم الزاوية في C، وكانت D نقطة على الوتر AB ، وكان CD يُعامد AB ، وقياس الزاوية DAC =° 65 درجة فما هو قياس كلّ من الزاويا: ACD ، , ABC ؟

الحل: مجموع زوايا المثلث ∆ACD =180، ومنه ADC+DAC+ACD =180،و 90+65+ACD =180، ومنه ACD=°25. بما أن AC يُعامد BC فإن الزاويتان ACB=90 درجة، وهي تساوي BCD + ACD ومنه: BCD+∠25=90، ومومنهBCD=°65. مجموع زوايا المثلث BDC=180، ومنه CBD BDC++ BCD=180، CBD+90+65=180، ومنه CBD=°25، والزاويتان ABC=CBD=°25.

المثال الثاني: إذا كان المثلث ABC مثلث متساوي الساقين حيث AB =AC وكان قياس الزاوية A=100° درجة، ما هو قياس الزاوية C؟

الحل: بما أن المثلث ABC مثلث متساوي الساقين فقياس الزاويتين B= C مجموع زوايا المثلث ABC=درجة 180، ومنه الزوايا A+B+C=180،والزوايا 100+C+C =180، ومنه 100+2×C=180، ومنه الزاوية C=(180-100)÷2، ومنه C=°40. وبما ان B=C بالتالي قياس B=°40 درجة.

المثال الثالث: هل من الممكن أن يكون هناك مثلث أطوال أضلاعه هي: 5 سم، 6 سم، 4 سم؟

الحل: نتحقق من تحقق الخاصة إذا كان مجموع أطوال أي ضلعين في هذا المثلث أكبر من الضلع الثالث فإن هذه الأضلاع تشكّل مثلثاً،

وعليه5+>4، 5+4>6، 4+6>5+٦، وبالتالي يُمكن لهذه الأضلاع أن تشكّل مثلثاً.

المثال الرابع: تم تقصير وتصغير أطوال أضلاع مثلث متساوي الأضلاع ليقل كل ضلع منها في طوله: 12سم، 13سم، 14سم، على الترتيب، وعليه أصبح هذا المثلث قائم الزاوية، جد طول كل ضلع من الأضلاع قبل تصغيرها وتقصيرها ..؟

الحل: نفترض أن x هو طول الأضلاع قبل التصغير، وعليه يكون طول أضلاع المثلث الأصلي بعد التقصير: (x-12)، (x-13)، (x-14). بما أنه تشكّل لدينا مثلث قائم الزاوية بعد تقصير الأضلاع، فإنه وبعد افتراض أن الضلع (x-12) هو الوتر؛ لأنه أطول الأضلاع، يمكن التعويض في نظريّة فيثاغورث لينتج أن: A²=B² + C² ~ x) -12)²= x)-14)²+(x-13)²، وومنهx²-24x+144= (x²-28x+196)+( x²-26x+169)، وبجمع الحدود المتشابهة ينتج أن: x²-30x+221، ومنه ينتج (x-13)(x-17)=0، وبحل هذه المعادلة (سوف نشرح حل المعادلات المختلفة بالتفصيل في مقالات لاحقة إن شآءالله) ينتج حلان إما ١٧ أو ١٣ وعليه قيمة x=17؛ لأنه لا يُمكن لأحد الأضلاع أن يكون سالباً، عند تعويض القيمة ١٣.

تعويض قيمة x)) للحصول على أطوال الأضلاع لينتج أن:x -12= 17-12 = 5سم. X-13 = 17-13 =4سم. x-14= 17-14 = 3سم.

المثال الخامس: هل يُمكن لزوايا مثلث أن يكون قياسها 90°، 60°، 30°؟

الحل: يجب أن يكون مجموع زوايا المثلث=180، فبجمع زوايا المثلث 90+60+30 ينتج أن مجموعها يساوي 180°، بالتالي يُمكن للمثلث أن يمتلك هذه الزوايا هذا المثال بسيط جداً لكت وارد أن يأتي في الامتحان وهام جداً..

المثال السادس: مثلث فيه الزاوية الثانية أكبر بمقدار ١٠ درجات من الزاوية الأولى، والزاوية الثالثة أكبر بمقدار ١٠درجات من الزاوية الثانية ما هو قياس الزوايا الثلاث؟

الحل: نفرض أن قياس الزاوية الأولى=x، وقياس الزاوية الثانية = x+10، وقياس الزاوية الثالثة =10+x)+10=س+20. مجموع زوايا المثلث =180، وبالتاليx + x+10))+(x+20)=180، ومنه x+303=180، وبالتالي س=180 -30 )÷3، فينتج أن قياس الزاوية الأولى 50x= . تعويض قيمة x لإيجاد قياس باقي الزوايا، قياس الزاوية الثانية=x +10=+10+ 55=60، وقياس الزاوية الثالثة= x+20=50+20=70، بالتالي ينتج أن قياس الزوايا هو: (50°، 60° 70 °).

المثال السابع: إذا كان قياس زوايا مثلث هي ثلاثة اعداد صحيحة موجبة متتاليةأي تأتي وراء بعضها مثل ١ ٢ ٣ ٤ ٥ وهكذا ، ما هو قياس هذه الزوايا؟

الحل: نفرض أن قياس الزاوية الأولى=x، وقياس الزاوية الثانية=x+1، وقياس الزاوية الثالثة=x+2. مجموع زوايا المثلث =180، وعليه: x+(x+1)+(x+2)=180، وبالتالي تصبح المعادلة: 3x+3=180، بالتالي x=(180-3)÷3، فينتج أن قياس الزاوية الأولى س=59. تعويض قيمة x لإيجاد قياس باقي الزوايا، قياس الزاوية الثانية=x+1=59+1=60، وقياس الزاوية الثالثة=x+2=59+2=61، بالتالي ينتج أن قياس الزوايا هو: (59°، 60°، 61°).

المثال الثامن خواص المثلثات : مثلث قائم الزاوية قياس زواياه غير القائمتين هو: x+1، 2x+5، ما هو قياس هذه الزوايا بالدرجات؟

الحل: مجموع زوايا المثلث =درجة 180، وعليه: 90+(x+1)+(2x+5)=180، ومنه 3x+96=180، وبالتالي x=(180-96)÷3، فينتج أن قيمة x=28. تعويض قيمة x لإيجاد قياس الزوايا، وعليه قياس الزاوية الثانية=x+1=28+1=29، وقياس الزاوية الثالثة=2x+5=(2×28)+5=61، وبالتالي ينتج أن قياس الزوايا الأخرى هو: (29°، 61°) يوجد عدد غير منتهي من التمارين والأمثلة أنصحكم بحل الكثير من التمارين والمسائل لزيادة أستيعاب هذا الدرس الهام وتدعيم الأفكار وزيادة المهارات في علم الرياضيات..

ختاماً :

للعناصر والأشكال الهندسية دور مهم وفعال في الحياة ولها الكثير من الاستخدامات وإذا تأملنا ماحولنا وجدنا أنه فب أبسط الأشياء والمعدات والآلات نستخدم الأشكال الهندسية المتنوعة والشهيرة ونلاحظ أستخدام شكل المثلث في كثير من الأستعمالات وخصوصاً لتحمل الأجهادات والضغط وغيرها من القوى المختلفة

ويوجد عدد كببر من الخواص والقوانين والمعادلات لحساب عناصر مجهولة في المثلث معرفة نوعه وطبيعته وخواصه سنتعرف عليها إن شآءالله في المقالات المقبلة مستقبلاً ..

أتمنى أن أكون قد قدمت الفائدة العلمية عن خواص المثلثات و أنواعها وأستخداماتها وكيفية حساب أطوال المتوسطات .. لاتنسوا الإعجاب بموقعنا المتواضع ومشاركتنا أرآكم في قسم التعليقات في الأسفل دمتم في أمان وطاعة الله والسلام عليكم ورحمة الله وبركاته .

شاهد ايضاً الأشكال الهندسية وخواصها2023